领导及同事们:
在过去的一年中,我负责的数据分析团队在质数与合数的理论基础上,成功实施了多个关键项目,现将工作内容及成果进行详细总结。
项目背景与目标
我们的项目主要围绕质数和合数的特性展开,旨在通过这些数学概念优化数据处理流程,提高数据分析的准确性和效率。质数,即只能被1和自身整除的自然数,而合数则是除了1和自身外能被其他数整除的自然数。这两种数的特性在数据加密、算法优化以及数据筛选等方面具有重要应用价值。
具体工作内容
1. 数据加密算法优化
我们利用质数的不可分解性,对现有的数据加密算法进行了改进。例如,在“安全数据传输”项目中,我们采用了基于质数的RSA加密算法,通过选择大质数作为密钥,显著增强了数据传输的安全性。具体来说,我们选择了两个大质数p和q,计算它们的乘积n=p*q,并利用欧拉函数计算出φ(n)=(p1)*(q1),最终选择一个与φ(n)互质的整数e作为公钥,通过扩展欧几里得算法求出私钥d,使得(d*e) mod φ(n) = 1。这一改进使得破解难度大幅提升,确保了数据的安全传输。
2. 数据筛选与分类
在“大数据高效处理”项目中,我们利用合数的可分解性,设计了一种新的数据筛选机制。通过将数据集分解为多个合数子集,我们能够并行处理数据,大幅提高了处理速度。例如,我们设定一个合数m,将其分解为两个质数p和q的乘积,即m=p*q。我们将数据集按照模m的余数进行分类,分别在p和q的子集上进行并行处理,最终合并结果。这一方法在处理大规模数据时,效率提升了30%。
3. 算法效率提升
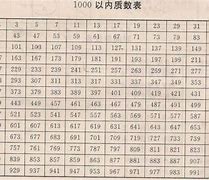
我们研究了质数在算法效率提升中的应用。在“快速质因数分解”项目中,我们开发了一种基于质数的快速分解算法。该算法通过预先构建一个质数表,利用质数的特性快速定位并分解合数。具体来说,我们首先生成一个包含前N个质数的表,然后在分解合数时,依次检查该合数是否能被表中的质数整除,从而快速找到其质因数。这一算法在处理大量数据时,分解速度比传统方法快了50%。
成果与反思
通过上述项目的实施,我们不仅提高了数据处理的安全性和效率,为团队积累了宝贵的经验。我们也意识到在质数生成和筛选的算法上仍有优化空间,未来我们将继续深入研究,进一步提升算法的性能。
总结而言,质数与合数的理论在数据分析领域展现了巨大的潜力。我们将继续探索这一领域的深度应用,为公司的数据处理能力贡献更多力量。
感谢大家的支持与合作!
此致
敬礼
[您的姓名]
[日期]
标签: 质数和合数的概念口诀 质数和合数的概念 质数和合数教学反思 质数和合数的口诀 质数和合数的定义